The bit operations are operations executed with number having a size of a "double-word" without any sign (an integer ranging between 0 and 4294967295) on the level of individual number bits (i.e. 32 bits on the whole for one number).

 

AND bit product

 

Individual bits of the AND operation result are set to the value of 1, if the corresponding bits of all operands are set to the value of 1, otherwise the bit is set to zero (value of 0).

 

OR bit sum

 

Individual bits of the OR operation result are set to the value of 1, if the corresponding bit of at least one operand is set to the value of 1, otherwise the bit is set to zero (value of 0).

 

XOR bit inversion

 

Individual bits of the XOR operation result are set to the value of 1, if the corresponding bit of an odd number of operands are set to the value of 1, otherwise the bit is set to zero (value of 0). To say it in other words: Bit 1 of each operand changes (flips, negates) the bit of the operation result, whereas bit 0 does not influence the operation result.

 

NOT bit complement

 

Individual bits of the NOT operation result are set to the value of 1, if the corresponding bit of the operand is not set to 1, otherwise the bit is set to zero (value of 0). To say it in other words: The value of each bit will change (be negated).

 

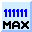maximum bit number (doubleword)

 

The value of the maximal bit number is 4294967295 (hexadecimal $FFFFFFFF).

 

bit rotate left

 

The bit rotation to the left brings about a shift of all operand bits one position towards higher bits accompanied with a carry of the most significant bit to the least significant one. For 2147483647 (i.e. $7FFFFFFF) and less the bit-rotate-left operation corresponds to the operation of doubling the number.

 

bit rotate right

 

The bit rotation to the right brings about a shift of all operand bits one position towards lower bits accompanied with a carry of the least significant bit to the most significant one. For even numbers the bit-rotate-right operation corresponds to the operation of dividing by two.